【GAMES101】图形学学习记录——着色
【GAMES101】图形学学习记录——着色(Shading)
简而言之,着色就是为物体附上不同材质的过程。
Blinn-Phong模型
Blinn-Phong模型简单地展示了一个着色点在受到光线照射时会表现出什么颜色。
输入:观测方向v,平面法线n,光照方向l,表面参数(颜色,反光度等)。
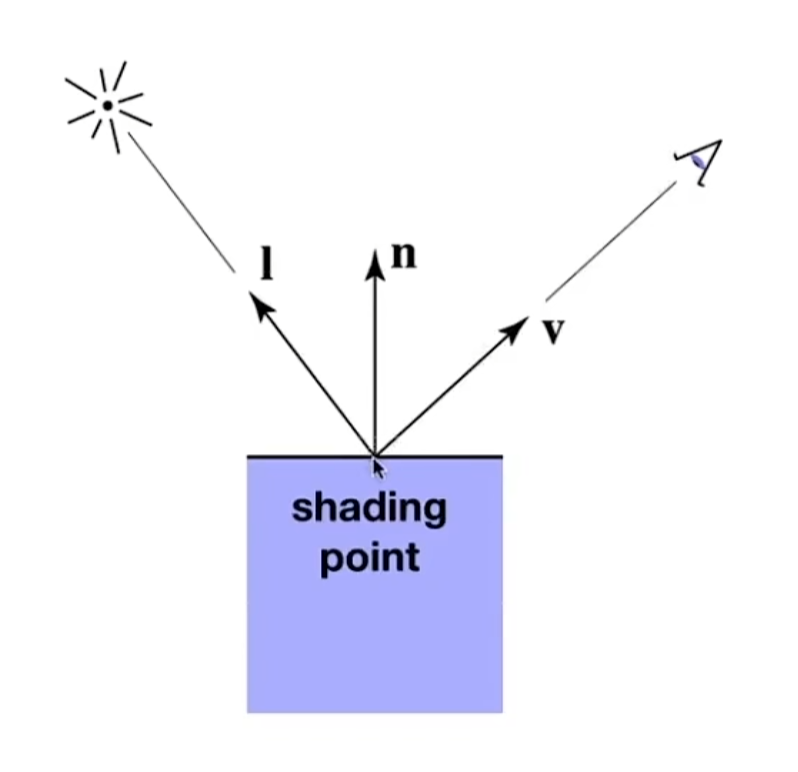
反射
在Blinn-Phong模型中,物体在受到光照后展现出的效果由三个部分组成:漫反射,高光反射,环境光照。
漫反射
光线照射在物体表面时向四周反射的现象被称为漫反射。公式如下:
镜面反射
当我们处于特定的角度观察较为光滑的物体时,会看到物体表面会有明亮的高光,这就是镜面反射产生的效果。
特定的角度为当观察方向(v)和镜面反射的方向(r)足够接近时(范围由材质决定)。
计算v和r的距离较为麻烦,因此我们可以用半程向量(h)和平面法线(n)之间的距离来代替。
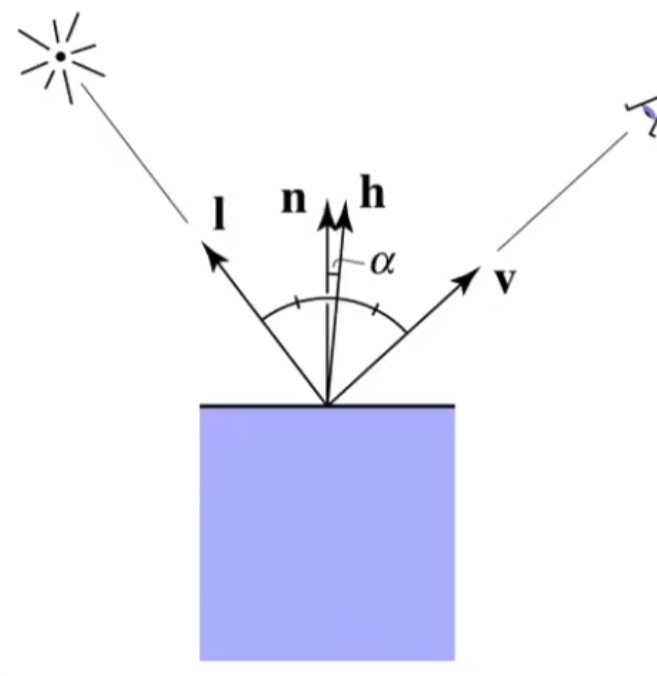
半程向量的计算公式以及高光反射的计算公式。
值得注意的是p这个参数。在现实生活中能看到高光的范围是很小的,但是因为余弦函数的曲线变化较为缓慢,即使观察距离和镜面反射角度相差较大,余弦值也仍然较高。通过进行p次方运算(p通常取120-150),可以是余弦函数曲线快速下降,保证只有在较小范围内能看到高光。
环境光照
顾名思义,环境光照是指环境中的光线照射产生的效果。公式如下:
Blinn-Phong反射
将以上三种反射相加就得到了Blinn-Phong模型中的反射结果。
着色频率
当确定了着色方式后,着色频率是接下来需要考虑的重要一环。着色频率决定了资源消耗和着色效果。如果着色频率过高,最终的着色效果会很好,但需要消耗大量资源;如果着色频率过低,消耗的资源相对较小,但效果可能不尽如人意。以下是几种典型的着色频率。
- flat shading:对于每一个平面,根据平面的法线进行着色。
- Gouraud shading:对平面的每个顶点根据顶点的法线进行着色,平面内部的着色由顶点着色结果插值得出。
- Phong shading:求出每个顶点的法线并进行着色,对内部的每个像素都进行插值。
如果我们知道了每个平面的法线,我们要如何得到每个顶点的法线?一种简单的做法是将与这个顶点相邻的平面的法线求平均:
图形管线(实时渲染管线)
图形管线(Graphics Pipeline)是指渲染时的一套固定流程。
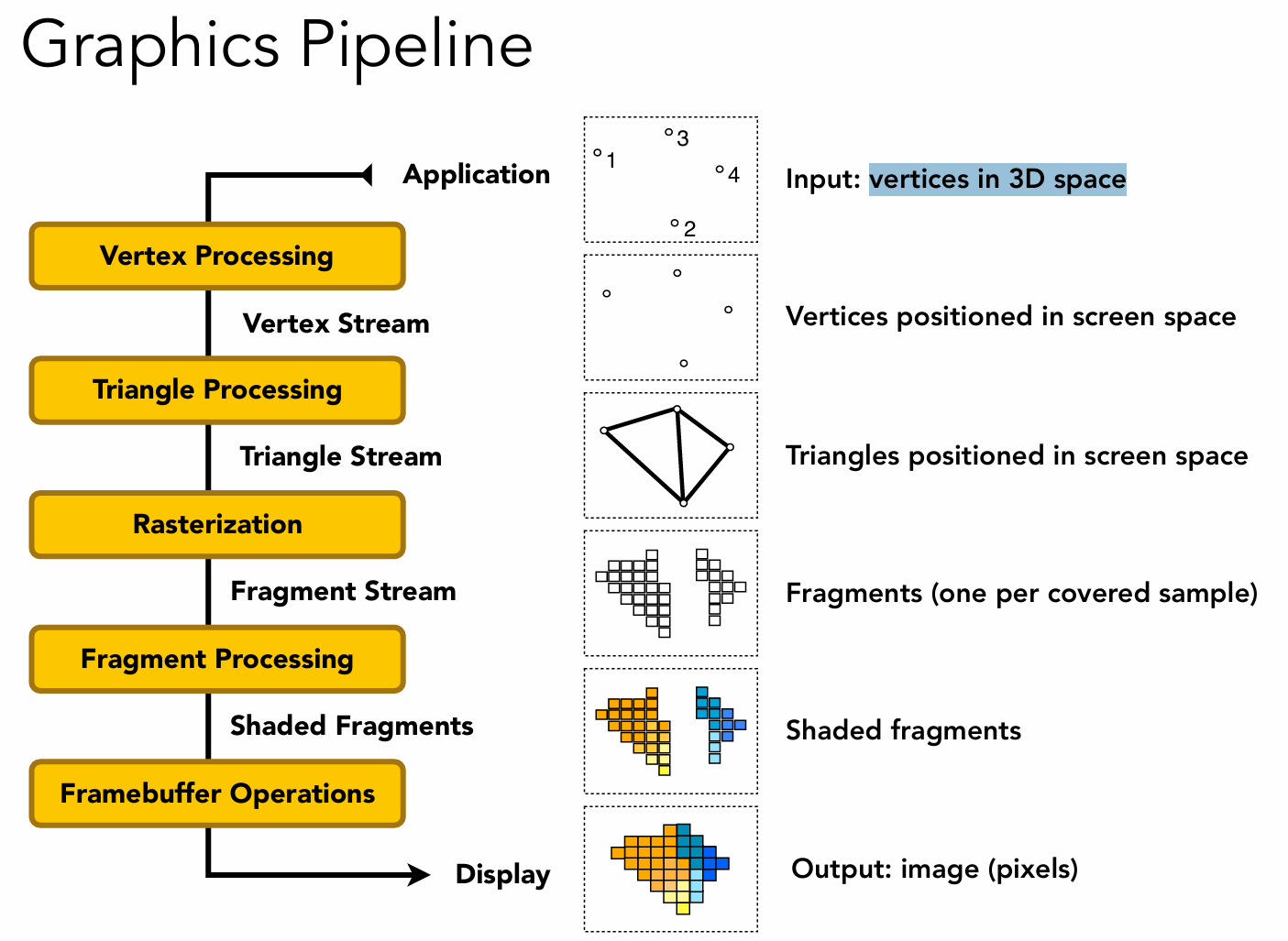
当输入一堆三维空间中的顶点后,经过顶点处理、三角形处理、光栅化、片元处理、帧缓冲操作后就得到了输出:一个图像(由一组像素组成)。
纹理映射
之前提到,一个着色点呈现出的效果和它的参数有关,但是我们不可能依次给每个着色点设置我们想要的参数。纹理映射(Texture Mapping)可以将二维的材质图包裹在三维物体的表面。以下是实现方法。
我们知道,三维物体是由一个个三角形组成的,那么我们可以将这些三角形映射二维材质图上的三角形中。这样一来,在进行纹理映射时,我们只需要找出三维物体的三角形和二维材质图的三角形之间的关系即可。我们使用uv坐标来实现。
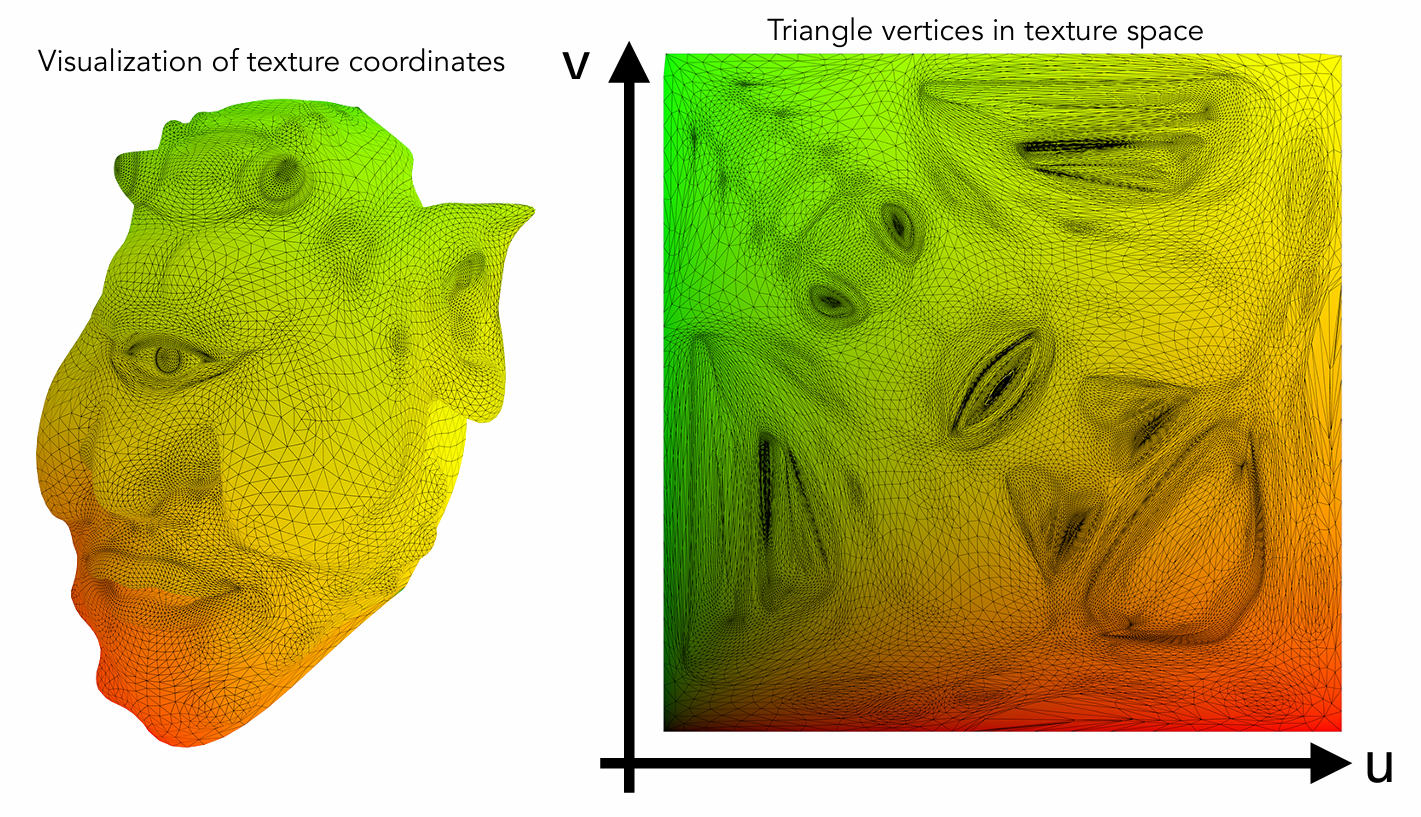
插值
之前我们提到过,可以利用插值的方法得到平面内部的一些值。当计算完三角形顶点的属性后,利用插值可以在三角形内部进行平滑的过渡。
插值的原理是三角形内部的每个点根据其在三角形中的位置都有一个重心坐标(α,β,γ)。对于三角形ABC来说:
重心坐标的求法是面积比:
对于任意要插值的属性V,计算公式如下:
纹理放大和纹理缩小
在理想情况下,物体大小和纹理大小应该是相同且一一对应的,但是在实际情况中,物体在不同的距离看起来会变大或变小,导致纹理和物体不能完全匹配,我们需要用一些方法来解决这个问题。
纹理放大
当物体过近时,纹理对于物体来说过小,物体上点可能不会被准确地映射到纹理上的点上,而是一些点之间。解决这个问题的方法是双线性插值。
首先我们需要了解什么是线性插值。对于两个点v0,v1之间的点x,它的插值为:
而双线性插值则是在二维平面上做插值。
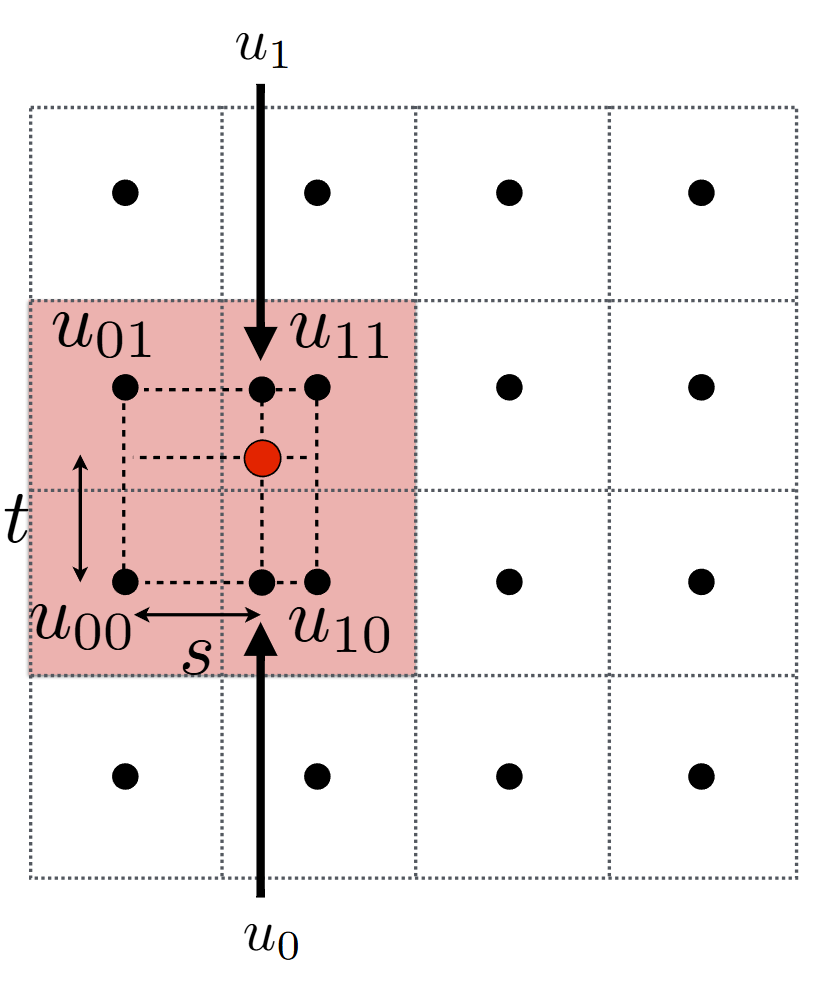
首先我们要先在x轴方向做两次插值,得到u0和u1的位置,再用这两个点做一次线性插值,即可得到双线性插值的结果,公式如下:
有一种精度更高的插值方法:Bicubic插值,对周围十六个点做插值。
纹理缩小
当物体距离过远时,一个像素映射到纹理上的区域过大,采样不足导致走样,这和之前光栅化部分说到的走样的原理是相同的。可以将像素划分为多个小像素,但开销过大。如果可以快速得到像素对应纹理上这一片区域的平均值,就可以在一定程度上解决这个问题。
Mipmap:这是一种快速,不准确,只针对正方形区域的范围查询。首先我们对纹理进行预处理,产生多层纹理,每一层纹理的分辨率都为之前的一半,直到1x1。在进行纹理映射时,只需要选择最接近的纹理即可。
各向异性过滤:不止是正方形,长宽可以不同比例。课程中没有具体描述实现过程。大致原理是对映射点周围方形8个或更多的像素进行取样,获得平均值平均后映射到像素点上。
纹理的应用
在现代的GPU中,我们可以将纹理理解成一块内存,我们可以在上面做各种操作(点查询、范围查询)。
环境光照
可以用纹理来映射任何环境中照射来的光(例如犹他茶壶)。通常假设环境光都是从无限远处照射而来。
我们可以把整个环境光都记录在一个球上,并像地球仪转换为世界地图一样将其展开。但是这样会导致球的上下两端展开后产生扭曲。一个解决方法是将球体替换成边长和球直径相同的正方体。
影响着色结果
之前,我们都用纹理来替代Blinn-Phong模型中的kd,来影响物体的颜色。其实,纹理也可以改变其他属性,例如凹凸贴图(法线贴图),我们可以用纹理记录物体每一个位置的相对高度(法线移动的距离和方向),来造成凹凸不平的效果。计算方法如下:

现在的做法:使用位移贴图,通过改变三角形的顶点位置来产生更逼真的效果。需要模型足够精细,三角形数量够多。
三维纹理
三维纹理不止存储物体表面的材质,还有三维空间任何一个点的材质。可以在三维空间中添加一个噪声函数,经过一系列处理后得到任意一点的效果。
存储之前计算好的结果
例如,在着色时我们不会考虑阴影等物体,当计算完阴影后,我们可以将环境光遮蔽贴图记录下来,并在之后直接应用。
