【GAMES101】图形学学习记录——变换
【GAMES101】图形学学习记录——变换
在正式开始学习计算机图形学之前,我们需要了解一些关于线性代数的基础知识。
点和向量的表示
我们通常用一个二维列向量来表示一个点的位置或者一个向量,例如:
矩阵的表示
矩阵的表示方式:
图形的变换
矩阵和向量之间可以进行加减乘除等运算,这里省略。我们知道,一个图形可以用一系列点来表示。如果我们想要对一个图形进行变换操作,我们只需要让这个图形的所有点移动到我们想要的位置即可。我们可以通过对这些点进行运算来实现这个操作。
镜像变换
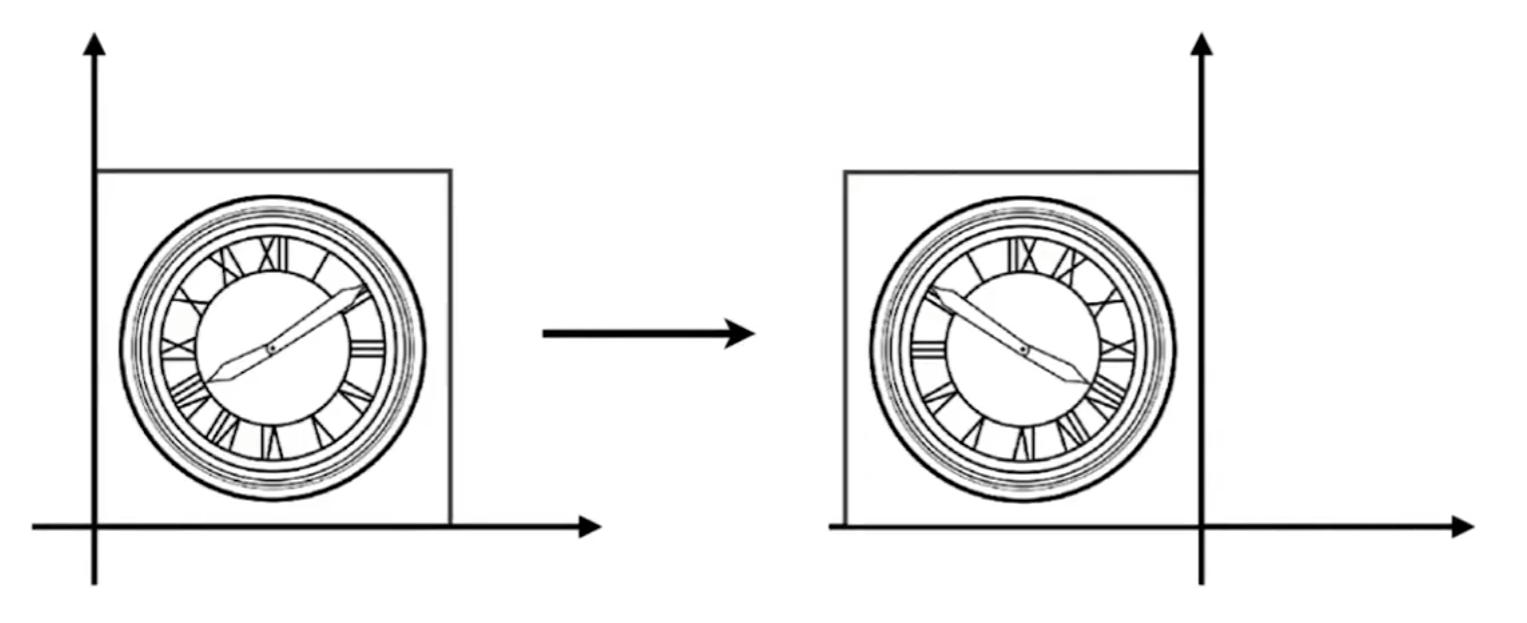
对于这个变换,我们只需要让x或y值变成相反数。
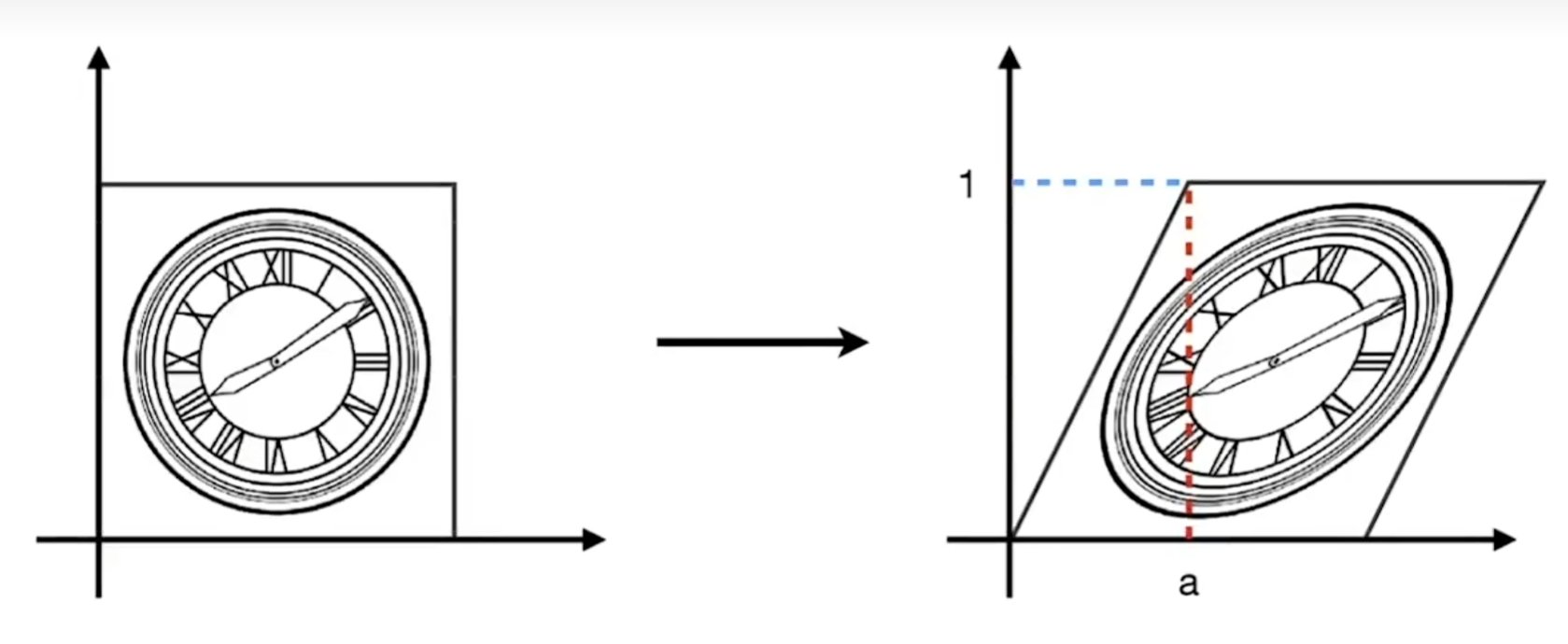
切变
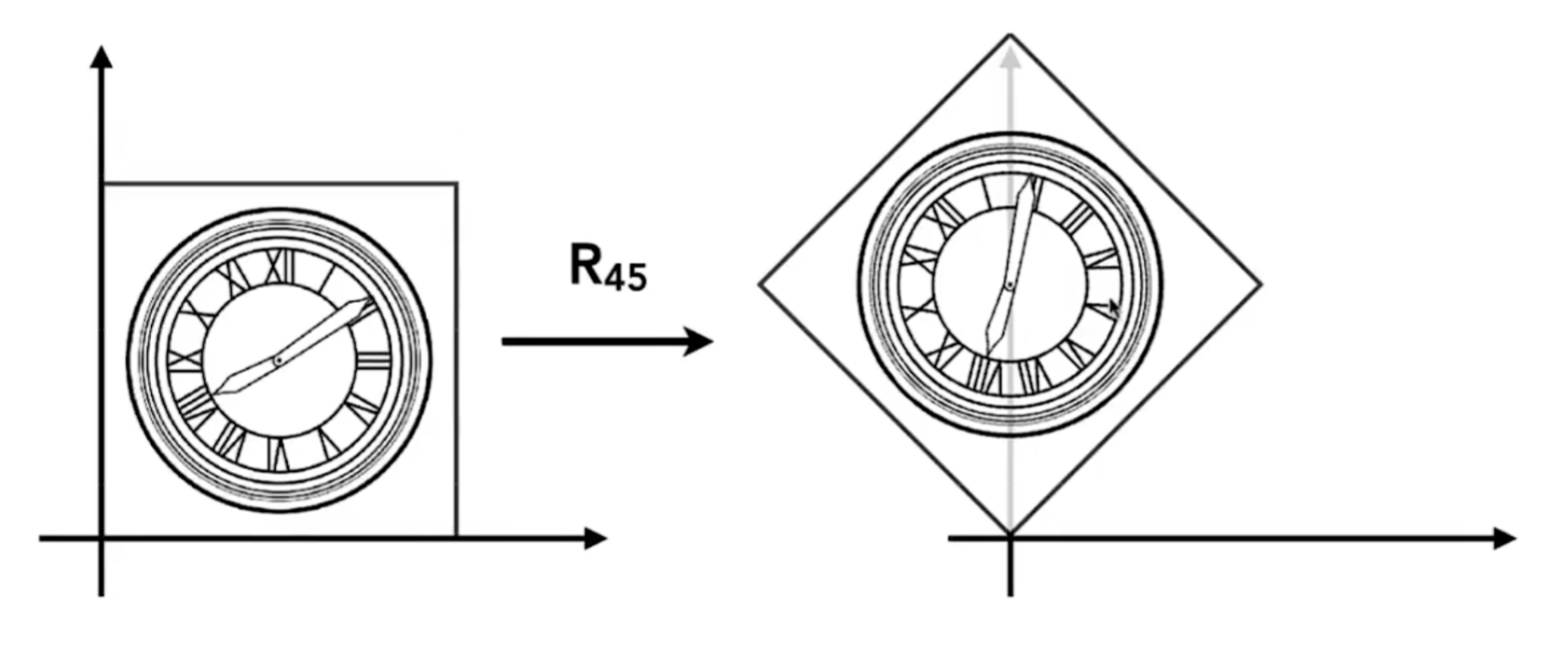
旋转
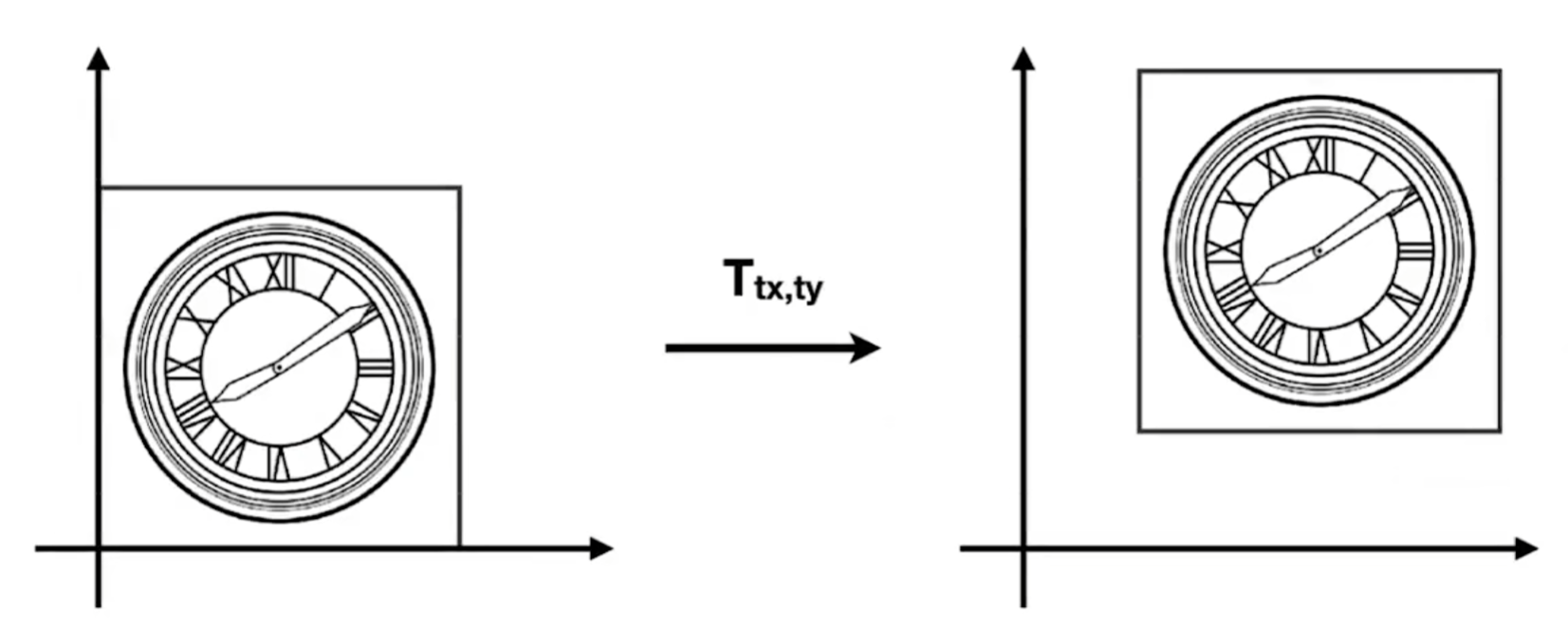
平移
齐次坐标
我们可以注意到,前三个变换都是用变换矩阵乘以点的形式,而平移操作需要我们用点的向量加上平移矩阵。有没有一种方法可以将平移操作也统一成乘法形式?
答案是齐次坐标。
我们将所有n维的矩阵和向量都加上一个维度,例如:
我们可以在多出来的这一个维度中表示平移的操作,例如:
而对于向量矩阵来说,多出来的这个维度也有其作用。例如下面这个向量:
当w=0时,这个向量矩阵表示的就是一个向量。当w=1时,这个向量矩阵表示的是一个点。
而当w!=0且w!=1时,它表示的如下的点:
对于前三种变换矩阵,我们只需要加上一个维度即可,例如旋转:
变换的组合
如果我们想对对象进行一系列变换,我们只需要依次对对象左乘变换即可,但是要注意顺序。
例如,我们想对X做变换M1,M2,…Mn,乘积的顺序应该是:
补充
三维空间中的旋转公式
绕x轴:
绕y轴:
绕z轴:
绕任意轴的旋转公式
观测变换
现在我们已经知道了在一个坐标空间中的物体是如何摆放和移动的,但是如果我们想要表示出我们是如何“看到”它们的,我们要怎么做呢?
例如,在现实生活中,火车的轨道是平行的,但是我们却能看到铁轨在远处交汇。通过观测变换,我们就能知道摄像机在指定的位置看到的物体是什么样的。
观测变换(MVP变换)分为:模型变换(模型摆放的位置)、视图变换(确定摄像机的位置和方向,并保证所有物体跟随摄像机移动)、投影变换(将三维空间的物体投影到二维平面上。
我们的重点是投影变换。
相机的摆放
以(0,0,0)为原点,将摄像机放在原点上,并以y轴方向为摄像机的上方向,使摄像机看向-z方向。这样摆放符合右手坐标系。
投影变换
投影变换分为两种:正交投影和透视投影。前者不遵循近大远小法则,而后者较为接近我们现实中看到的情况。
正交投影
假设物体在如下的立方体中,我们要做的是将其移动到正则立方体((-1,1)^3)中。之后如何将其显示在屏幕上,我们会在下一节“光栅化”中讲解。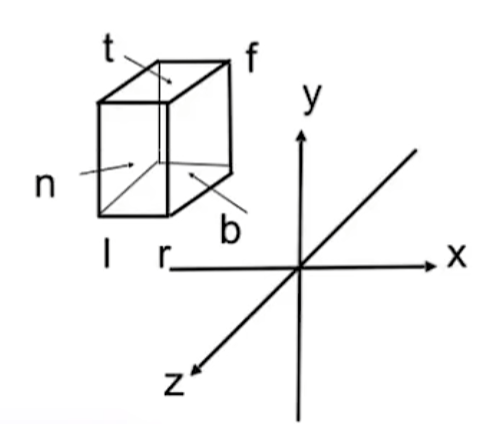
这个过程比较简单,我们只需要将其移动到原点,再进行缩放。变换矩阵如下:
透视投影及推导
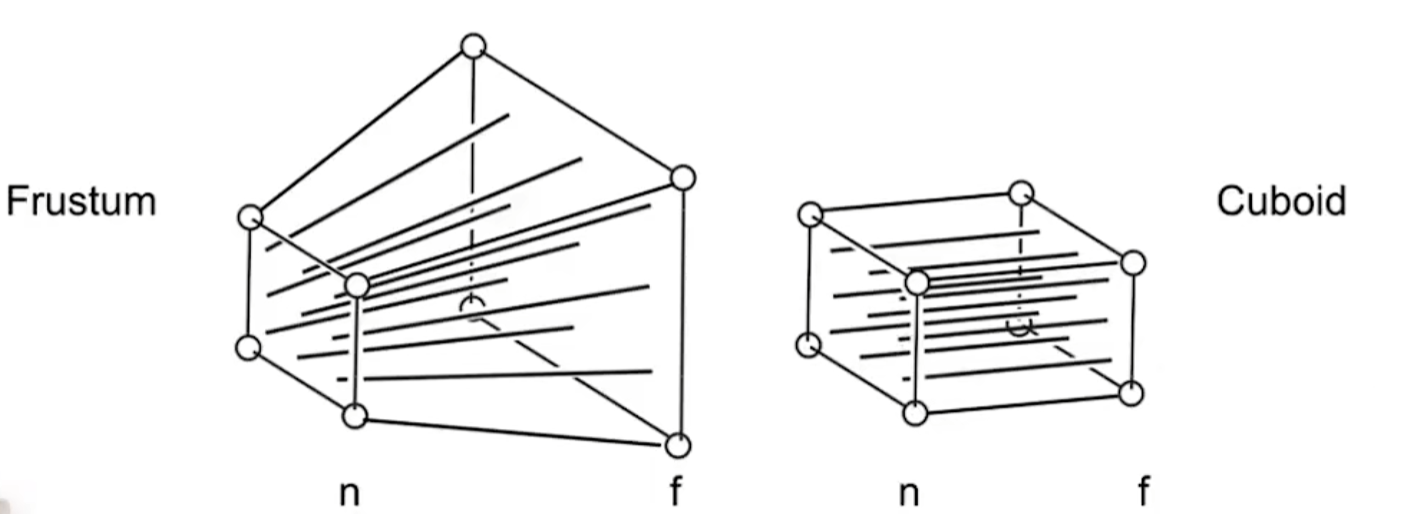
在透视投影中,我们要投影的是如下所示的一个棱台。直接做投影比较困难,但是我们可以将其“压缩”成一个长方体后再对其做正交投影。下面给出推导过程。
所谓的压缩是指我们需要将较远的大平面压缩为和n处小平面相同大小。这里有三个原则:
- 近平面上的任意一点都不会发生改变
- 远平面上的任意一点的z值都不会发生改变
- 远平面上的中心点不会发生改变
对于任意一点(x,y,z),我们假设它投影到近平面后的点为(x’,y’,z’),从侧面看去,可以得到如下的一个相似三角形: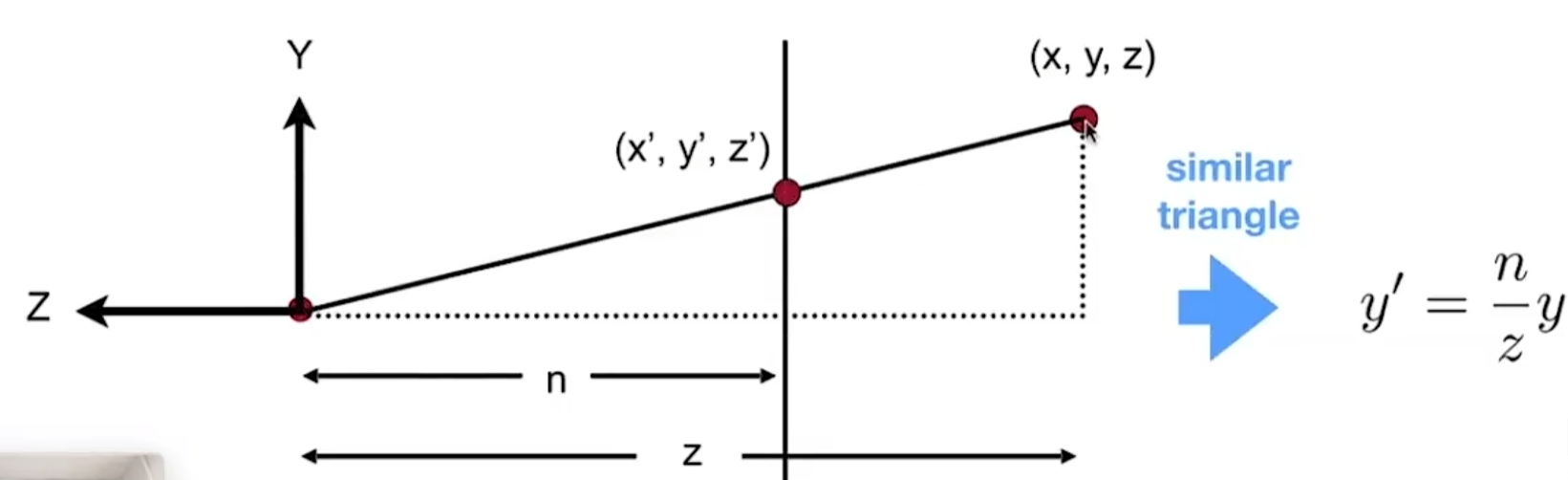
根据相似三角形的性质,我们可以得到:
同理可得:
因此,我们的目标就是找到一个变换矩阵使得(x,y,z)转换成(x’,y’,x’),也可以写做如下形式:
通过这两个关系,我们已经可以推出变换矩阵的一部分。
剩下的一个行向量,我们需要用之前说过的三个原则来解出。
对于近平面上的点,它在变换前和变换后的z值都是n,可以得出:
对于远平面上的点,它在变换前和变换后的z值都是f,同理可得:
通过这两个方程,我们就可以解出A和B的值:
最终得到的变换矩阵如下:
之后的过程和正交投影相同。
